• Statistical Calculation Crossword Clue
• Statistical Calculations

The G8X92AA from HP is a cutting-edge new generation statistical calculator that boasts of features like a full-color display, multi touch control options like the keyboard or the touch screen and the ability to switch between different types of views (Graphical or numbers) with dedicated keys.

Source code:Lib/statistics.py

This module provides functions for calculating mathematical statistics ofnumeric (Real-valued) data.

The module is not intended to be a competitor to third-party libraries suchas NumPy, SciPy, orproprietary full-featured statistics packages aimed at professionalstatisticians such as Minitab, SAS and Matlab. It is aimed at the level ofgraphing and scientific calculators.

Unless explicitly noted, these functions support int,float, Decimal and Fraction.Behaviour with other types (whether in the numeric tower or not) iscurrently unsupported. Collections with a mix of types are also undefinedand implementation-dependent. If your input data consists of mixed types,you may be able to use map() to ensure a consistent result, forexample: map(float,input_data).

1. Provides a collection of 106 free online statistics calculators organized into 29 different categories that allow scientists, researchers, students, or anyone else to quickly and easily perform accurate statistical calculations. Also provides a complete set of formulas and scientific references for each statistical calculator.
2. Statistical Sample Size Calculator The article “ Sample Examples – The Calculator in Action ” provides guidance for using the Calculator below in various scenarios. For discussion of Fannie Mae’s new 6 (or 3) month statement standard, please see this post.
3. The calculator actually is capable of other statistical modes which we will cover in another lesson. Note that all calculations for this course can be done in statistical mode. Once you place the calculator in this mode, it will remain so until the mode is changed.
4. Make use of our Statistics Calculators to calculate basic to complicated statistical data from a set of numerical values in a simple way. Just have a glance at the topics listed here and pick the required free statistics online calculator and you are good to go with learning the concept & finding the solutions to your lengthy calculations.

Averages and measures of central location¶

These functions calculate an average or typical value from a populationor sample.

Measures of spread¶

These functions calculate a measure of how much the population or sampletends to deviate from the typical or average values.

Function details¶

Note: The functions do not require the data given to them to be sorted.However, for reading convenience, most of the examples show sorted sequences.

Return the sample arithmetic mean of data which can be a sequence or iterable.

The arithmetic mean is the sum of the data divided by the number of datapoints. It is commonly called “the average”, although it is only one of manydifferent mathematical averages. It is a measure of the central location ofthe data.

If data is empty, StatisticsError will be raised.

Some examples of use:

Note

The mean is strongly affected by outliers and is not a robust estimatorfor central location: the mean is not necessarily a typical example ofthe data points. For more robust measures of central location, seemedian() and mode().

The sample mean gives an unbiased estimate of the true population mean,so that when taken on average over all the possible samples,mean(sample) converges on the true mean of the entire population. Ifdata represents the entire population rather than a sample, thenmean(data) is equivalent to calculating the true population mean μ.

Convert data to floats and compute the arithmetic mean.

This runs faster than the mean() function and it always returns afloat. The data may be a sequence or iterable. If the inputdataset is empty, raises a StatisticsError.

New in version 3.8.

Convert data to floats and compute the geometric mean.

The geometric mean indicates the central tendency or typical value of thedata using the product of the values (as opposed to the arithmetic meanwhich uses their sum).

Raises a StatisticsError if the input dataset is empty,if it contains a zero, or if it contains a negative value.The data may be a sequence or iterable.

No special efforts are made to achieve exact results.(However, this may change in the future.)

New in version 3.8.

Return the harmonic mean of data, a sequence or iterable ofreal-valued numbers.

The harmonic mean, sometimes called the subcontrary mean, is thereciprocal of the arithmetic mean() of the reciprocals of thedata. For example, the harmonic mean of three values a, b and cwill be equivalent to 3/(1/a+1/b+1/c). If one of the valuesis zero, the result will be zero.

The harmonic mean is a type of average, a measure of the centrallocation of the data. It is often appropriate when averagingrates or ratios, for example speeds.

Suppose a car travels 10 km at 40 km/hr, then another 10 km at 60 km/hr.What is the average speed?

Suppose an investor purchases an equal value of shares in each ofthree companies, with P/E (price/earning) ratios of 2.5, 3 and 10.What is the average P/E ratio for the investor’s portfolio?

StatisticsError is raised if data is empty, or any elementis less than zero.

The current algorithm has an early-out when it encounters a zeroin the input. This means that the subsequent inputs are not testedfor validity. (This behavior may change in the future.)

New in version 3.6.

Return the median (middle value) of numeric data, using the common “mean ofmiddle two” method. If data is empty, StatisticsError is raised.data can be a sequence or iterable.

The median is a robust measure of central location and is less affected bythe presence of outliers. When the number of data points is odd, themiddle data point is returned:

When the number of data points is even, the median is interpolated by takingthe average of the two middle values:

This is suited for when your data is discrete, and you don’t mind that themedian may not be an actual data point.

If the data is ordinal (supports order operations) but not numeric (doesn’tsupport addition), consider using median_low() or median_high()instead.

Return the low median of numeric data. If data is empty,StatisticsError is raised. data can be a sequence or iterable.

The low median is always a member of the data set. When the number of datapoints is odd, the middle value is returned. When it is even, the smaller ofthe two middle values is returned.

Use the low median when your data are discrete and you prefer the median tobe an actual data point rather than interpolated.

Return the high median of data. If data is empty, StatisticsErroris raised. data can be a sequence or iterable.

The high median is always a member of the data set. When the number of datapoints is odd, the middle value is returned. When it is even, the larger ofthe two middle values is returned.

Use the high median when your data are discrete and you prefer the median tobe an actual data point rather than interpolated.

Return the median of grouped continuous data, calculated as the 50thpercentile, using interpolation. If data is empty, StatisticsErroris raised. data can be a sequence or iterable.

In the following example, the data are rounded, so that each value representsthe midpoint of data classes, e.g. 1 is the midpoint of the class 0.5–1.5, 2is the midpoint of 1.5–2.5, 3 is the midpoint of 2.5–3.5, etc. With the datagiven, the middle value falls somewhere in the class 3.5–4.5, andinterpolation is used to estimate it:

Optional argument interval represents the class interval, and defaultsto 1. Changing the class interval naturally will change the interpolation:

This function does not check whether the data points are at leastinterval apart.

CPython implementation detail: Under some circumstances, median_grouped() may coerce data points tofloats. This behaviour is likely to change in the future.

See also

• “Statistics for the Behavioral Sciences”, Frederick J Gravetter andLarry B Wallnau (8th Edition).

• The SSMEDIANfunction in the Gnome Gnumeric spreadsheet, including this discussion.

Return the single most common data point from discrete or nominal data.The mode (when it exists) is the most typical value and serves as ameasure of central location.

If there are multiple modes with the same frequency, returns the first oneencountered in the data. If the smallest or largest of those isdesired instead, use min(multimode(data)) or max(multimode(data)).If the input data is empty, StatisticsError is raised.

mode assumes discrete data and returns a single value. This is thestandard treatment of the mode as commonly taught in schools:

The mode is unique in that it is the only statistic in this package thatalso applies to nominal (non-numeric) data:

Changed in version 3.8: Now handles multimodal datasets by returning the first mode encountered.Formerly, it raised StatisticsError when more than one mode wasfound.

Return a list of the most frequently occurring values in the order theywere first encountered in the data. Will return more than one result ifthere are multiple modes or an empty list if the data is empty:

New in version 3.8.

Return the population standard deviation (the square root of the populationvariance). See pvariance() for arguments and other details.

Return the population variance of data, a non-empty sequence or iterableof real-valued numbers. Variance, or second moment about the mean, is ameasure of the variability (spread or dispersion) of data. A largevariance indicates that the data is spread out; a small variance indicatesit is clustered closely around the mean.

If the optional second argument mu is given, it is typically the mean ofthe data. It can also be used to compute the second moment around apoint that is not the mean. If it is missing or None (the default),the arithmetic mean is automatically calculated.

Use this function to calculate the variance from the entire population. Toestimate the variance from a sample, the variance() function is usuallya better choice.

Raises StatisticsError if data is empty.

Examples:

If you have already calculated the mean of your data, you can pass it as theoptional second argument mu to avoid recalculation:

Decimals and Fractions are supported:

Note

When called with the entire population, this gives the population varianceσ². When called on a sample instead, this is the biased sample variances², also known as variance with N degrees of freedom.

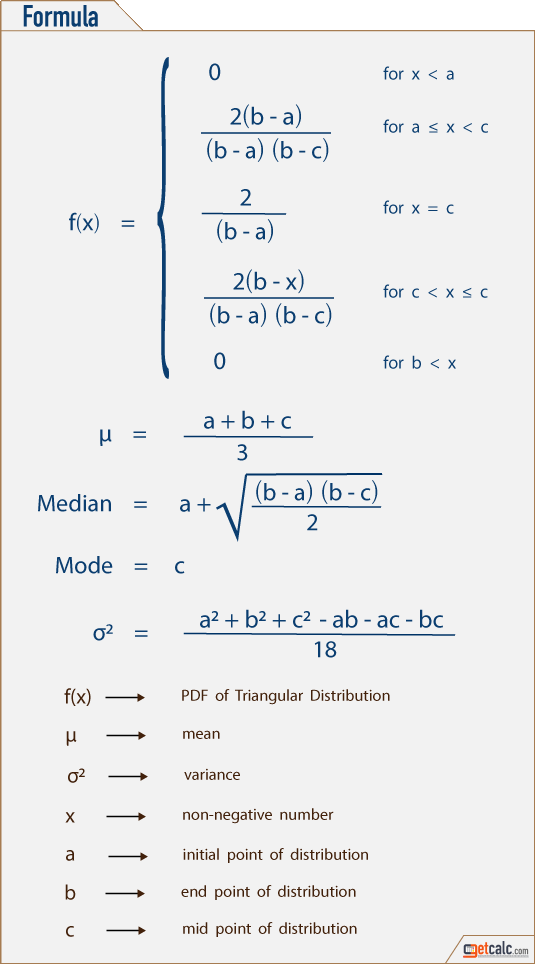
If you somehow know the true population mean μ, you may use thisfunction to calculate the variance of a sample, giving the knownpopulation mean as the second argument. Provided the data points are arandom sample of the population, the result will be an unbiased estimateof the population variance.

Return the sample standard deviation (the square root of the samplevariance). See variance() for arguments and other details.

Return the sample variance of data, an iterable of at least two real-valuednumbers. Variance, or second moment about the mean, is a measure of thevariability (spread or dispersion) of data. A large variance indicates thatthe data is spread out; a small variance indicates it is clustered closelyaround the mean.

If the optional second argument xbar is given, it should be the mean ofdata. If it is missing or None (the default), the mean isautomatically calculated.

Use this function when your data is a sample from a population. To calculatethe variance from the entire population, see pvariance().

Raises StatisticsError if data has fewer than two values.

Examples:

If you have already calculated the mean of your data, you can pass it as theoptional second argument xbar to avoid recalculation:

This function does not attempt to verify that you have passed the actual meanas xbar. Using arbitrary values for xbar can lead to invalid orimpossible results.

Decimal and Fraction values are supported:

Note

This is the sample variance s² with Bessel’s correction, also known asvariance with N-1 degrees of freedom. Provided that the data points arerepresentative (e.g. independent and identically distributed), the resultshould be an unbiased estimate of the true population variance.

If you somehow know the actual population mean μ you should pass it to thepvariance() function as the mu parameter to get the variance of asample.

Divide data into n continuous intervals with equal probability.Returns a list of n-1 cut points separating the intervals.

Set n to 4 for quartiles (the default). Set n to 10 for deciles. Setn to 100 for percentiles which gives the 99 cuts points that separatedata into 100 equal sized groups. Raises StatisticsError if nis not least 1.

The data can be any iterable containing sample data. For meaningfulresults, the number of data points in data should be larger than n.Raises StatisticsError if there are not at least two data points.

The cut points are linearly interpolated from thetwo nearest data points. For example, if a cut point falls one-thirdof the distance between two sample values, 100 and 112, thecut-point will evaluate to 104.

The method for computing quantiles can be varied depending onwhether the data includes or excludes the lowest andhighest possible values from the population.

The default method is “exclusive” and is used for data sampled froma population that can have more extreme values than found in thesamples. The portion of the population falling below the i-th ofm sorted data points is computed as i/(m+1). Given ninesample values, the method sorts them and assigns the followingpercentiles: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%.

Setting the method to “inclusive” is used for describing populationdata or for samples that are known to include the most extreme valuesfrom the population. The minimum value in data is treated as the 0thpercentile and the maximum value is treated as the 100th percentile.The portion of the population falling below the i-th of m sorteddata points is computed as (i-1)/(m-1). Given 11 samplevalues, the method sorts them and assigns the following percentiles:0%, 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, 100%.

New in version 3.8.

Exceptions¶

A single exception is defined:

Subclass of ValueError for statistics-related exceptions.

NormalDist objects¶

NormalDist is a tool for creating and manipulating normaldistributions of a random variable. It is aclass that treats the mean and standard deviation of datameasurements as a single entity.

Normal distributions arise from the Central Limit Theorem and have a wide rangeof applications in statistics.

Returns a new NormalDist object where mu represents the arithmeticmean and sigmarepresents the standard deviation.

If sigma is negative, raises StatisticsError.

A read-only property for the arithmetic mean of a normaldistribution.

A read-only property for the median of a normaldistribution.

A read-only property for the mode of a normaldistribution.

A read-only property for the standard deviation of a normaldistribution.

A read-only property for the variance of a normaldistribution. Equal to the square of the standard deviation.

Statistical Calculation Crossword Clue

Makes a normal distribution instance with mu and sigma parametersestimated from the data using fmean() and stdev().

The data can be any iterable and should consist of valuesthat can be converted to type float. If data does notcontain at least two elements, raises StatisticsError because ittakes at least one point to estimate a central value and at least twopoints to estimate dispersion.

Generates n random samples for a given mean and standard deviation.Returns a list of float values.

If seed is given, creates a new instance of the underlying randomnumber generator. This is useful for creating reproducible results,even in a multi-threading context.

Using a probability density function (pdf), computethe relative likelihood that a random variable X will be near thegiven value x. Mathematically, it is the limit of the ratio P(x<=X<x+dx)/dx as dx approaches zero.

The relative likelihood is computed as the probability of a sampleoccurring in a narrow range divided by the width of the range (hencethe word “density”). Since the likelihood is relative to other points,its value can be greater than 1.0.

Using a cumulative distribution function (cdf),compute the probability that a random variable X will be less than orequal to x. Mathematically, it is written P(X<=x).

Compute the inverse cumulative distribution function, also known as thequantile functionor the percent-pointfunction. Mathematically, it is written x:P(X<=x)=p.

Finds the value x of the random variable X such that theprobability of the variable being less than or equal to that valueequals the given probability p.

Measures the agreement between two normal probability distributions.Returns a value between 0.0 and 1.0 giving the overlapping area forthe two probability density functions.

Divide the normal distribution into n continuous intervals withequal probability. Returns a list of (n - 1) cut points separatingthe intervals.

Set n to 4 for quartiles (the default). Set n to 10 for deciles.Set n to 100 for percentiles which gives the 99 cuts points thatseparate the normal distribution into 100 equal sized groups.

Compute theStandard Scoredescribing x in terms of the number of standard deviationsabove or below the mean of the normal distribution:(x-mean)/stdev.

Instances of NormalDist support addition, subtraction,multiplication and division by a constant. These operationsare used for translation and scaling. For example:

Dividing a constant by an instance of NormalDist is not supportedbecause the result wouldn’t be normally distributed.

Since normal distributions arise from additive effects of independentvariables, it is possible to add and subtract two independent normallydistributed random variablesrepresented as instances of NormalDist. For example:

New in version 3.8.

NormalDist Examples and Recipes¶

NormalDist readily solves classic probability problems.

For example, given historical data for SAT exams showingthat scores are normally distributed with a mean of 1060 and a standarddeviation of 195, determine the percentage of students with test scoresbetween 1100 and 1200, after rounding to the nearest whole number:

Statistical Calculations

Find the quartiles and deciles for the SAT scores:

To estimate the distribution for a model than isn’t easy to solveanalytically, NormalDist can generate input samples for a MonteCarlo simulation:

Normal distributions can be used to approximate Binomialdistributionswhen the sample size is large and when the probability of a successfultrial is near 50%.

For example, an open source conference has 750 attendees and two rooms with a500 person capacity. There is a talk about Python and another about Ruby.In previous conferences, 65% of the attendees preferred to listen to Pythontalks. Assuming the population preferences haven’t changed, what is theprobability that the Python room will stay within its capacity limits?

Normal distributions commonly arise in machine learning problems.

Wikipedia has a nice example of a Naive Bayesian Classifier.The challenge is to predict a person’s gender from measurements of normallydistributed features including height, weight, and foot size.

We’re given a training dataset with measurements for eight people. Themeasurements are assumed to be normally distributed, so we summarize the datawith NormalDist:

Next, we encounter a new person whose feature measurements are known but whosegender is unknown:

Starting with a 50% prior probability of being male or female,we compute the posterior as the prior times the product of likelihoods for thefeature measurements given the gender:

The final prediction goes to the largest posterior. This is known as themaximum a posteriori or MAP: